The Blockchain Hype Cycle

Blockchain is a system design that de-centralizes control over data. In practice, the data is often a "ledger," or a chronological list of transactions. This is what underpins cryptocurrencies like Bitcoin, Ether, and Dogecoin - a set of transactions that, when summed together, define a currency balance for a particular user. This ledger can be extended to transactions of other digital objects, like sports highlights, tweets, and iconic memes. The value of blockchain is its ability to verify transactions without requiring parties to fully trust each other. It does this by giving many different computers the ability to verify transactions.

In the last couple of months, Blockchain has gotten a LOT of publicity. NFT's famously were sold for large sums of money. Coinbase, one of the biggest platforms for trading cryptocurrencies (which live on blockchains), IPO'd. Many high-profile investors have expressed both positive and negative opinions of cryptocurrency and blockchain as a technology.

In a word, blockchain has a lot of hype.

Gartner, a global research and advisory company, has a tool tailor-made to frame this kind of explosive publicity: the Gartner Hype Cycle.

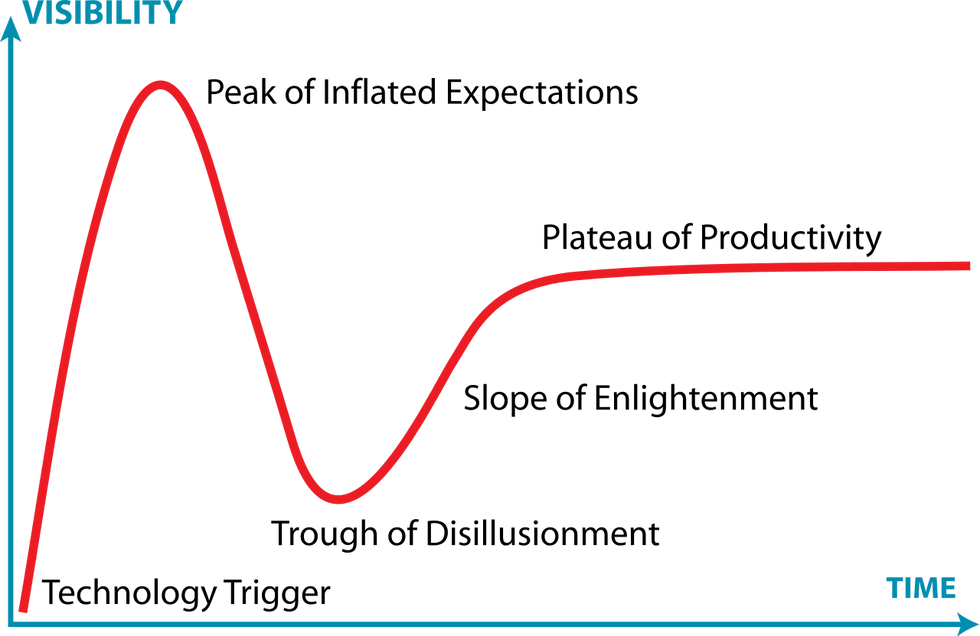
In short, the Hype Cycle is meant to capture the dynamics of technology development and expectations. The tool is purely qualitative, so its dimensions are entirely nebulous. However, it approximates an underlying model of how the behavior of adopters, developers, and the media can lead to wide swings in a technology's appraised value. As part of a research seminar in System Dynamics, I worked on creating a stylized dynamic model of the hype and publicity surrounding new technologies. In this post, I'll try to fit that analysis to Blockchain.

System Dynamics is a modeling framework that applies concepts from controls theory to the social sciences. Because System Dynamics models are basically collections of real behavioral mechanisms, it's possible to create a System Dynamics model without data. Stylized models can abstract away much of the complexity of the real world to gain rich insights into the way these mechanisms interact in the real world. For that reason, it's used in a wide variety of contexts, including public health, finance, public policy, ecology, and supply chain planning.

I'll spare you the mathy details of the model, which can be found in the document at the bottom of this article. In essence, the model is a set of differential equations that, together, define the movement of a dynamic system. This movement revolves around three variables: the "True Ability" of a technology, its "Forecasted Future Ability," and the number of "Adopters."

• As a technology is adopted by more people, the True Ability grows according to an exponential decay function. Over time, as the True Ability improves, it improves more slowly. This is essentially the effect of Diminishing Returns.

• The Forecasted Future Ability uses a simple trend function based on the growth rate of the True Ability to predict a technology's ability a fixed amount of time in the future.

• The population adopts the technology based on the Forecasted Future Ability, which is a prediction of how advanced the technology will be in the future.

• As more people adopt the product, the growth of the user base accelerates the learning and development rate of the technology. In some cases, the technology also has some exogenous learning rate, meaning it can improve without feedback from adopters.

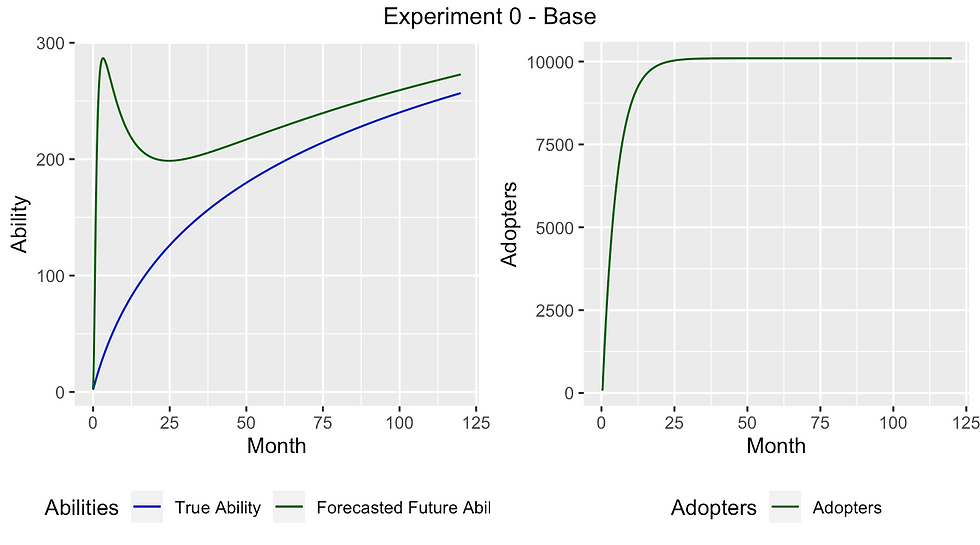
• The original model was run with a population of about 10,000 potential adopters, with a modeling horizon of 120 months.

The nice thing about this model is how simple it is. Its assumptions won't hold in every case, but it's a compelling and parsimonious way to understand how different system characteristics affect our outcomes.

After building the model, it's common to test it by performing a set of experiments. In the paper, you'll see six different runs of the model, each with different tuning parameters and different results. For this post, I'll just focus on a couple.

In the base case, we see the exponentially decaying learning rate inducing the same kind of behavior presented in the Gartner Hype Cycle. The Adoption population quickly grows to the entire population. This applies to technologies that have low opportunity cost, and will be adopted even with low Forecasted Future Ability. This may apply well to technologies like 5G, where adoption requires little to no investment compared to the alternative.

Not every technology is easy to adopt. This is especially true of enterprise products that require significant investment to fully implement. As a result, the required Forecasted Future Ability is significantly higher for this adoption. By adjusting the preference function to model this change, we observe a different adoption behavior. The size of the Adopter population quickly plateaus, before adoption resumes in an S-shaped curve. This S-curve is a commonly discussed concept in literature surrounding innovation.

In another experiment, I shortened the forecast length. This dampened a lot of the forecast volatility, since forecasts were less overfit on the most recent changes in a technology's ability. As a result of this decrease in volatility, the Adopters population grows quickly to saturation, and doesn't show that pause in adoption before moving into an S-curve. This suggests that S-curves are driven by the volatility of expectations.

Both of these findings can be applied to blockchain. Blockchain's forecast horizon will likely be much longer - people are making decades-out predictions into the future of blockchain. This suggests an enormous amount of volatility in its Future Forecasted Ability, which is consistent with current events; Bitcoin has instantly gone from a niche investment vehicle to part of the daily news. Blockchain is a technology that requires a lot of up-front investment, so the tipping point and preference heterogeneity will be very high. This suggests we'll soon see a plateau in adoption, which will grow later in that S-curve shape.

So if I had to make a hypothesis based on these results, my guess is that we'll soon see a plateau in blockchain adoption as people become more realistic about its short-term capability. Over time, it will slowly-but-steadily develop in capability, will be adopted by more of the general population via new platforms and apps, and will eventually become something we interact with in our everyday lives.

After coming to this conclusion, I wasn't fully satisfied. After all I've said about the dangers of intuition and cognitive bias, it would be hypocritical to jump to conclusions

based on my Monday-afternoon extrapolations of a model I haven't touched in a year. So followed the advice I assumed I'd give and dug up the model, corrected an equation or two in the paper, and reran it.

Of course, nothing is ever as simple as just rerunning a model. Many elements of the model don't fit blockchain, so I made the following adjustments to the model.

• Blockchain will likely take multiple decades to fully mature, requiring a longer modeling horizon.

• As a novel technology, the learning rate will decay at a slower rate than more mature technologies.

• Adoption of the technology will unearth problems more quickly, meaning adoption-driven learning will occur more quickly.

• The minimum adoption time is significantly longer. Since it's a new technology, people and companies will have to spend more time to develop it and incorporate it into their processes

• Predictions on its eventual capability (like the ones I've made in this post) will happen for much longer forecast horizons.

• Finally, the barrier to adoption means the tipping point and heterogeneity parameters need to be increased.

The results of the simulation after these adjustments are below.

IMPORTANT DISCLAIMER: I didn't use any data for this. So you shouldn't take these results to the bank, or to your Bitcoin wallet, or your investment portfolio. All this represents is me feeding some "reasonable" estimates of parameters into a model that simulates the underlying dynamics. It ignores some pertinent concerns, like the possibility of regulation, the impact of multiple competing blockchains (as bars to network effects), and the energy cost of existing blockchains. It's not a precise prediction. With a little more time and motivation, I'd collect data and use an optimization algorithm to tune my parameters to fit that data - that's a model I'd be comfortable investing with.

Caveats aside, I think there are a couple things worth taking away from this exercise.

First, it's an example of how System Dynamics can be a powerful tool for modeling an uncertain future. The underlying mechanisms simulated in the model are built on solid principles of human behavior. The model's simplicity lends itself to showing the behavior of these mechanisms when they work together. Despite its simplicity, the model has captured some very nonlinear system behavior and made it easier to comprehend.

Second, it's a warning of the current blockchain hype. Blockchain as a technology is here to stay. But it won't be as prevalent in the near-term as some Bitcoin Bulls may lead you to believe. It's likely that we'll see a decrease in confidence and a corresponding slowing of adoption in the near term.

In case you want to understand the model more deeply, poke holes in its results, or replicate it yourself, I've attached the term paper I submitted last year, along with a list of the parameters I used for the blockchain model. Happy modeling!

Term_Paper.docx

Download DOCX • 877KB

BlockchainParameters.docx

Download DOCX • 13KB